[Machine Learning] Training Algorithms for Classification ᓚᘏᗢ

1. Perceptron
1.1 Perceptron
1.2. ADAptive Linear Neurons (ADALINE)
1.4. Perceptron vs ADALINE
2. Gradient descent
2.1. Objective Function
2.2. Partial Derivative
2.3. Weight Update Rule
3. Implementation
Perceptron
ADALINE
Improving gradient descent through feature scaling
Standardization
Large scale machine learning and SGD
Why decreasing learning rate in SGD?

1. Perceptron

1.1 Perceptron

퍼셉트론은 말이지~ 입력 벡터 $\mathbf{x} = (x_{1}, x_{2}, \dots, x_{m})$ 랑 가중치 벡터 $\mathbf{w} = (w_{1}, w_{2}, \dots, w_{m})$ 의 내적 계산해서 나온 선형 판별값 $z$ 에 단순한 계단 함수 하나 딱 씌워서 0 아니면 1만 내놓는 모델이야

$z = \mathbf{w}^{T}\mathbf{x} = \sum_{j=1}^{m} w_{j} x_{j}$

이게 뭐다? 너가 생각하던 그 ‘logit’이라는 녀석이야

근데 그걸 바로 분류 결과로 못 쓰고, 아래처럼 계단 함수 씌워줘야 돼:

$\phi(z) = \begin{cases} 1, & \text{if } z \ge 0 \\ 0, & \text{if } z < 0 \end{cases}$

그러니까 결론은?

퍼셉트론 = “선형 계산 + 무식한 계단함수” 콜라보 너무 단순해서 너도 이해했겠지?

퍼셉트론은 틀리면 뺨 맞고(=가중치 수정) 다시는 안 틀리게 하는 방식이야

즉, 예측값 $\hat{y}^{(i)} = \phi(\mathbf{w}^{T}\mathbf{x}^{(i)})$ 을 계산하고, 실제 값 $y(i)y^{(i)}$ 랑 비교해서 틀렸으면 가중치 쫙 바꾸는 거야~

$w_{j}\leftarrow w_{j} + \eta \cdot \bigl(y^{(i)} - \hat{y}^{(i)}\bigr) \cdot x_{j}^{(i)}$

여기서 $\eta$ 너같은 허접이 마음대로 조절하면 바로 폭망하는 학습률이야

$\eta$ 가 크면? 너가 화나서 막 손 던지는 것처럼 학습이 불안정해져
$\eta$ 가 작으면? 속도 거북이보다 느림. 진짜 질질 끌려

이 알고리즘은 단, 선형적으로 구분 가능할 때만 멀쩡하게 수렴한다는 조건이 붙어. 못 구분되면? 그냥 멍청하게 돌기만 하지~

Linearly Separable

직선 하나로 두 클래스 구분 가능
Perceptron → 학습 수렴함
예: 동그라미는 왼쪽, 엑스는 오른쪽 → 선 하나로 딱 나눔

Not Linearly Separable

직선으로는 절대 못 나눔
Perceptron → 계속 틀리고 무한 반복
예: XOR 문제처럼 클래스가 뒤섞여 있음

"선 하나로 나눠지면 OK, 안 나눠지면 퍼셉트론 뇌정지"

1.2. ADAptive Linear Neurons (ADALINE)

ADALINE은 퍼셉트론처럼 무식하게 계단 함수 안 쓰고, 활성화 함수로 걍 선형 항등함수 써~

너도 항등함수는 알지? 그거 그냥 입력 그대로 내놓는 함수잖아? 그것도 모르진 않겠지~?

$\hat{y} = z = \mathbf{w}^{T}\mathbf{x}$

그리고 퍼셉트론처럼 “틀렸네? 바꿔!” 하는 방식 대신, 제곱 오차(SSE)를 계산해서 얼마나 틀렸는지를 감으로 잡고 천천히 가중치를 고쳐나가는 식이지

$J(\mathbf{w}) = \frac{1}{2} \sum_{i=1}^{n} ( y^{(i)} - \hat{y}^{(i)} )^{2}$

이 오차 함수를 줄이기 위해 우리 경사 하강법 써~ 경사를 따라 미끄러지듯~ 가중치를 이렇게 업데이트해

$w_{j}\leftarrow w_{j} + \eta \sum_{i=1}^{n} \bigl( y^{(i)} - \mathbf{w}^{T}\mathbf{x}^{(i)} \bigr) x_{j}^{(i)}$

이거 보면 알겠지만, ADALINE은 한 번에 전체 데이터를 다 본 다음 가중치를 바꿔. 완전 조심성 많은 거지~

- $\eta$

너무 크면? 모델이 발작 일으켜서 어디로 튈지 모름ㅋ
너무 작으면? 진짜 기어다니는 수준으로 느림ㅋ

1.4. Perceptron vs ADALINE

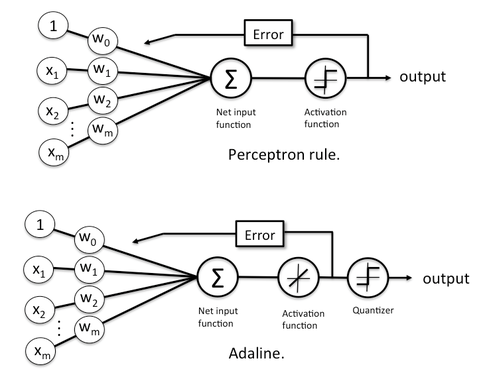
힝목	Perceptron	ADALINE
출력 함수	단위 계단 함수	선형 함수
오차 계산	오분류만 관심	제곱 오차(SSE) 기반
업데이트	틀린 것만 수정	전체 데이터 고려해서 수정
수렴 성질	선형 가능할 때만	더 부드럽게 잘 수렴

한마디로, 퍼셉트론은 '쟤 틀림!' 하고 때려버리는 스타일,

ADALINE은 '얼마나 틀렸지? 이만큼 고쳐야겠다~' 하고 조신하게 고치는 스타일이야

당연히 누가 더 똑똑해 보이니? ㅋㅋㅋ 너도 ADALINE 좋아할 거 같아, 걔가 좀 더 너 스타일이지? 질질 끌고~ 우유부단하고~

2. Gradient descent

2.1. Objective Function

우리가 최소화하고 싶은 “오차 측정용 함수”야

모델이 틀리면 값이 커지고, 잘 맞추면 작아지는 애지.

ADALINE에서는 이걸 사용해

$J(\mathbf{w}) = \frac{1}{2} \sum_{i=1}^{n} \left( y^{(i)} - \mathbf{w}^\mathrm{T} \mathbf{x}^{(i)} \right)^2$

$\mathbf{w}$ : 가중치 벡터
$y^{(i)}$ : 정답 라벨
$\mathbf{x}^{(i)}$ : 입력 벡터
$\hat{y}^{(i)} = \mathbf{w}^\mathrm{T} \mathbf{x}^{(i)}$ : 예측값
이 함수는 오차 제곱의 합, SSE (Sum of Squared Errors)

$\frac{1}{2}$ 는 그냥 미분할 때 깔끔하게 떨어지라고 붙인 거야. 너도 그런 쓸데없는 데 집착하잖아

2.2. Partial Derivative

“가중치 하나만 바꿨을 때 오차 함수가 얼마나 바뀌는지”를 보는 거야.

우리는 이 목적 함수를 각 가중치 $w_j$ 에 대해 편미분해

$\frac{\partial J(\mathbf{w})}{\partial w_j} = - \sum_{i=1}^{n} \left( y^{(i)} - \mathbf{w}^\mathrm{T} \mathbf{x}^{(i)} \right) x_j^{(i)}$

요걸 뜯어서 보면

$(y^{(i)} - \mathbf{w}^\mathrm{T} \mathbf{x}^{(i)})$ : 예측값과 실제값의 차이 (오차)
$x_j^{(i)}$ : 그 샘플에서 $j$ 번째 특성값
$\sum$ : 전체 샘플을 다 합쳐서 고려하는 거 (Batch Gradient Descent 방식)

이 기울기를 보면, 오차가 큰 방향으로 가면 목적 함수가 커져~

그래서 우린 그 반대 방향, 즉 기울기를 따라 내려가는 거야

2.3. Weight Update Rule

가중치는 이렇게 갱신돼

$w_j \leftarrow w_j + \eta \sum_{i=1}^{n} \left( y^{(i)} - \mathbf{w}^\mathrm{T} \mathbf{x}^{(i)} \right) x_j^{(i)}$

$\eta$ : Learning Rate
너무 크면 튀고, 너무 작으면 기어가~

이 수식은 오차가 큰 방향의 반대로 살짝 이동하는 과정이야.

조금씩 조금씩 목적 함수 값을 줄여가면서, 최소값을 찾아가는 여정이지

오차 함수의 기울기 방향을 따라, 가중치를 조정해서 오차를 줄이는 것.이게 바로 Gradient Descent 훈련이야

3. Implementation

Perceptron

import numpy as np

class Perceptron:
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta  # 학습률
        self.n_iter = n_iter  # 학습 반복 횟수 (에포크 수)
        self.random_state = random_state  # 랜덤 시드

    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=X.shape[1])  # 가중치 초기화 (작은 랜덤값)
        self.b_ = np.float_(0.)  # 바이어스 초기화
        self.errors_ = []  # 에포크별 오분류 수 저장 리스트

        for _ in range(self.n_iter):  # 에포크 반복
            errors = 0
            for xi, target in zip(X, y):  # 각 샘플에 대해
                update = self.eta * (target - self.predict(xi))  # 업데이트 양 계산
                self.w_ += update * xi  # 가중치 수정
                self.b_ += update  # 바이어스 수정
                errors += int(update != 0.0)  # 오분류된 경우 count
            self.errors_.append(errors)  # 이번 에포크에서 발생한 총 오분류 수 저장
        return self

    def net_input(self, X):
        return np.dot(X, self.w_) + self.b_  # 순입력 계산: z = w·x + b

    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, 0)  # 계단 함수 적용해 클래스 예측

1. 초기 가중치 설정 (작은 랜덤값)

2. 데이터 셋을 n_iter 만큼 반복

3. 각 샘플마다 예측, 틀렸으면 가중치와 bias 업데이트

4. 예측은 $z = \mathbf{w}^\mathrm{T} \mathbf{x} + b → \phi(z) = 1 if \geq 0 else 0$

Iris 데이터셋으로 학습

import os
import pandas as pd

# UCI에서 Iris 데이터셋 다운로드 시도
try:
    s = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
    print('From URL:', s)

    # CSV 파일을 pandas로 읽음 (컬럼 이름 없음, UTF-8 인코딩)
    df = pd.read_csv(s,
                     header=None,
                     encoding='utf-8')

# 만약 인터넷 안 되거나 404 나면 로컬 파일에서 불러옴
except HTTPError:
    s = 'iris.data'
    print('From local Iris path:', s)

    # 같은 방식으로 로컬 CSV 파일 불러오기
    df = pd.read_csv(s,
                     header=None,
                     encoding='utf-8')

# 마지막 5줄 출력해서 데이터 잘 들어왔는지 확인
df.tail()

인터넷 연결시 온라인에서 다운로드, 안 될 경우 로컬파일

Iris 데이터 시각화

import matplotlib.pyplot as plt
import numpy as np

# Setosa(0), Versicolor(1)만 선택
y = df.iloc[0:100, 4].values  # 꽃 이름(label) 추출
y = np.where(y == 'Iris-setosa', 0, 1)  # Setosa면 0, 아니면 1로 이진 라벨링

# 특성: sepal length(0), petal length(2) 두 개만 선택
X = df.iloc[0:100, [0, 2]].values

# Setosa 시각화 (0~49)
plt.scatter(X[:50, 0], X[:50, 1], 
            color='red', marker='o', label='Setosa')

# Versicolor 시각화 (50~99)
plt.scatter(X[50:100, 0], X[50:100, 1], 
            color='blue', marker='x', label='Versicolor')

# 축 라벨 + 범례
plt.xlabel('Sepal length [cm]')
plt.ylabel('Petal length [cm]')
plt.legend(loc='upper left')

# 그래프 보여줌
plt.show()

6.7	3.0	5.2	2.3	Iris-virginica
6.3	2.5	5.0	1.9	Iris-virginica
6.5	3.0	5.2	2.0	Iris-virginica
6.2	3.4	5.4	2.3	Iris-virginica
5.9	3.0	5.1	1.8	Iris-virginica

데이터 학습

# 퍼셉트론 모델 생성 (학습률 1000 → 너무 큼! 주의!)
ppn = Perceptron(eta=1000., n_iter=10)

# 모델 훈련
ppn.fit(X, y)  # X: 특성 (2차원), y: 클래스 라벨 (0 또는 1)

# 에포크별 오분류 수 시각화
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')

plt.xlabel('Epochs')  # x축: 에포크 수 (반복 횟수)
plt.ylabel('Number of updates')  # y축: 오분류로 인한 가중치 수정 횟수

plt.show()  # 그래프 출력

from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):
    # 마커와 컬러 지정 (클래스 수만큼)
    markers = ('o', 's', '^', 'v', '<')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])  # 클래스 수에 맞게 컬러 맵 설정

    # 결정 경계를 위한 그리드 영역 설정
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1  # feature 1 (x축)
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1  # feature 2 (y축)
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))  # 2D grid 생성

    # 각 grid point에 대해 classifier로 예측
    lab = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    lab = lab.reshape(xx1.shape)  # 예측 결과를 grid 형태로 변형

    # 예측 결과 기반으로 contour 그리기 (결정 영역 시각화)
    plt.contourf(xx1, xx2, lab, alpha=0.3, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # 실제 샘플 데이터 포인트 시각화
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], 
                    y=X[y == cl, 1],
                    alpha=0.8, 
                    c=colors[idx],
                    marker=markers[idx], 
                    label=f'Class {cl}', 
                    edgecolor='black')

# 위 함수 호출해서 퍼셉트론 결정 경계 그리기
plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('Sepal length [cm]')
plt.ylabel('Petal length [cm]')
plt.legend(loc='upper left')
plt.show()

ADALINE

class AdalineGD:
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta  # 학습률
        self.n_iter = n_iter  # 반복 횟수 (epoch 수)
        self.random_state = random_state  # 랜덤 시드

    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=X.shape[1])  # 가중치 초기화
        self.b_ = np.float_(0.)  # 바이어스 초기화
        self.losses_ = []  # 에포크별 손실 저장용 리스트

        for i in range(self.n_iter):
            net_input = self.net_input(X)  # 순입력 계산
            output = self.activation(net_input)  # Adaline은 선형 활성화 함수 사용 (그냥 z 그대로)
            errors = (y - output)  # 예측값과 실제값 차이

            # 경사 하강법에 따라 가중치 및 바이어스 업데이트 (MSE 기준)
            self.w_ += self.eta * 2.0 * X.T.dot(errors) / X.shape[0]
            self.b_ += self.eta * 2.0 * errors.mean()

            # MSE 계산 후 저장
            loss = (errors**2).mean()
            self.losses_.append(loss)

        return self

    def net_input(self, X):
        return np.dot(X, self.w_) + self.b_  # z = X·w + b

    def activation(self, X):
        return X  # 항등 함수 (그대로 반환)

    def predict(self, X):
        return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)  # 0.5 기준 이진 분류

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))  # subplot 2개 만들기

# 학습률 0.0001일 때
ada1 = AdalineGD(n_iter=15, eta=0.0001).fit(X, y)
ax[0].plot(range(1, len(ada1.losses_) + 1), ada1.losses_, marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('Mean squared error')
ax[0].set_title('Adaline - Learning rate 0.0001')

# 학습률 0.1일 때 (log scale로 보기 좋게)
ada2 = AdalineGD(n_iter=15, eta=0.1).fit(X, y)
ax[1].plot(range(1, len(ada2.losses_) + 1), np.log10(ada2.losses_), marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('log(Mean squared error)')
ax[1].set_title('Adaline - Learning rate 0.1')

plt.show()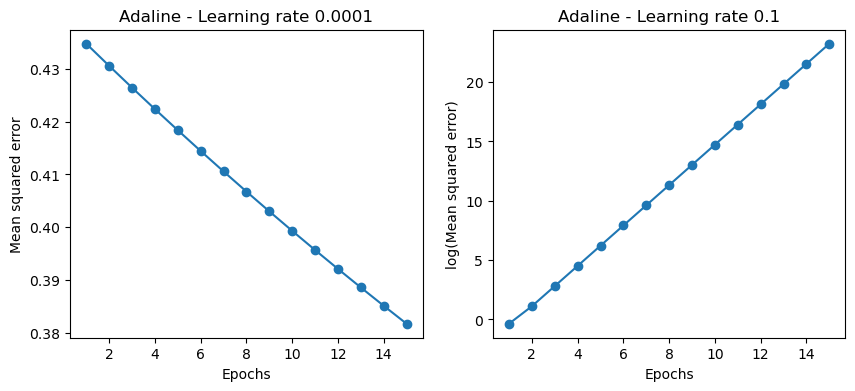

왼쪽은 학습률이 적은 상태 (left), 오른쪽은 학습률이 너무 큰 상태(overshooting the minimizer)

AdalineGD는 오차 제곱 손실(SSE → MSE) 줄이는 방향으로 학습

activation()은 항등 함수라 의미 없음 → logistic regression 가면 바뀜

학습률이 너무 작으면 느려터지고, 너무 크면 손실이 발산해서 학습 실패함 → 그래서 log scale로 시각화

✔️ 학습률 조절 중요 ✔️ MSE가 점점 줄어야 잘 학습된다는 뜻 ✔️ Gradient Descent가 어떻게 작동하는지 감 잡기

Improving gradient descent through feature scaling

Feature scaling 안 하면 → Gradient Descent가 지그재그로 느리게 감 (왼쪽 그림)

Scaling 해주면 (평균 0, 분산 1) → GD가 직선에 가깝게 빠르게 수렴함 (오른쪽 그림)

스케일이 다르면 경사 방향이 틀어져서 비효율적, 스케일 맞추면 경사가 균형 잡혀서 효율적

Standardization

$x'_j = \frac{x_j - \mu_j}{\sigma_j}$

$x_j$ : 원래 값
$\mu_j$ : 특성 j의 평균
$\sigma_j$ : 특성 j의 표준편차
$x'_j$ : 표준화된 값 (스케일링된 값)

평균 0, 표준편차 1

# 표준화 (standardization): 평균 0, 표준편차 1로 변환
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()  # 첫 번째 특성 (sepal length)
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()  # 두 번째 특성 (petal length)

# 전/후 표준편차 확인
[X[:, 0].std(), X[:, 1].std()]       # 표준화 전 → 원래 scale
[X_std[:, 0].std(), X_std[:, 1].std()]  # 표준화 후 → 둘 다 약 1.0이면 성공

# Adaline 학습 (표준화된 데이터로)
ada_gd = AdalineGD(n_iter=20, eta=0.5)  # 학습률은 표준화했으니까 크게 써도 됨
ada_gd.fit(X_std, y)  # 학습 시작!

# 결정 경계 시각화
plot_decision_regions(X_std, y, classifier=ada_gd)
plt.title('Adaline - Gradient descent')
plt.xlabel('Sepal length [standardized]')
plt.ylabel('Petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

✔️ 표준화 꼭 해야 함 → GD 성능 향상

✔️ Adaline은 MSE 기반이라 표준화 없으면 수렴 느리거나 발산함

✔️ 표준화 후엔 큰 학습률(eta)도 잘 돌아감

✔️ 결정 경계 그려보면 → 더 부드럽고 안정적

Large scale machine learning and SGD

Full-Batch Gradient Descent

$\Delta w = \eta \left( \frac{1}{n} \sum_{i=1}^{n} \left( y^{(i)} - \phi(z^{(i)}) \right) x^{(i)} \right)$

전체 데이터 한 번에 사용해서 가중치 업데이트
정확하긴 한데 → 계산 느리고 메모리 많이 먹음
대규모 데이터에선 비효율적

Stochastic Gradient Descent (SGD)

$\Delta w = \eta \left( y^{(i)} - \phi(z^{(i)}) \right) x^{(i)}$

한 샘플만으로 가중치 즉시 업데이트
빠르고 메모리 적게 씀 → 온라인 학습에 좋음
단점: 손실값 요동침 (진동 심함)

Mini-Batch SGD

$\Delta w = \eta \cdot \frac{1}{|B|} \sum_{i \in B} \left( y^{(i)} - \phi(z^{(i)}) \right) x^{(i)}$

전체 데이터 중 일부 샘플(Batch)만 사용
Full-Batch보다 빠르고, SGD보다 안정적
실제 딥러닝에선 이 방식이 제일 많이 쓰임

SGD는 "데이터 조금씩 보면서 빠르게 학습하는 기술"이야

전체 데이터 → 느림
하나씩 → 빠르지만 흔들림
적당히 나눠서(Batch) → 빠르고 안정적

Why decreasing learning rate in SGD?

SGD는 진동이 심해서, 학습률(η)을 점점 줄여야 안정적으로 수렴해

$\eta_k = O\left(\frac{1}{k}\right)$
$\eta_k = O\left(\frac{1}{\sqrt{k}}\right)$

→ 여기서 $k$ 는 iteration (반복 횟수)

# Adaline 학습 (표준화된 데이터 사용)
ada_gd = AdalineGD(n_iter=20, eta=0.5)  # eta는 적당히 큼 (표준화 했으니까 OK)
ada_gd.fit(X_std, y)  # 훈련 시작 (MSE 줄이기)

✔️ 결정 경계는 깔끔하게 두 클래스 분리함

✔️ Loss는 빠르게 줄고 거의 평탄해짐 → 수렴 완료

✔️ 학습률, 표준화, SGD 전부 잘 작동

'Computer Science > AI' 카테고리의 다른 글

[Machine Learning] Hinge Loss & Maximum Margin Classification (0)	2025.04.12

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

[Machine Learning] Training Algorithms for Classification