미리 요약. ARIA CPA를 통해 마스터키를 추출하려면 키스케쥴링상 점멸식이 사용 가능한 128비트 블록을 최소 2개 추출해야 한다.
필자는 128비트 환경에서 ek1, ek13을 추출, 조합해 마스터키를 추출하는 글을 작성하였다.
주어진 정보 (4)
1. 암호 알고리즘 정보 (ARIA-128)
2. Plaintext
3. Ciphertext
4. Power Trace
보통 부채널 공격에서는 1번 암호 알고리즘 정보는 따로 찾는 것이다.
1번의 정보가 주어지지 않아도 SPA 또는 입력값 CPA로 암호 알고리즘의 정보를 알 수 있을 것이다.
추후 입력값 CPA, 사이퍼 CPA등 따로 정리한 문서를 만들겠다.
Single(float32) 값으로 저장되어있는 ARIA 전력 파형이다. 자료형과 엔디안에 항상 주의해야 한다. 현재 주어진 파일에는 전력 파형 길이와 개수가 헤더로 입력되어있다
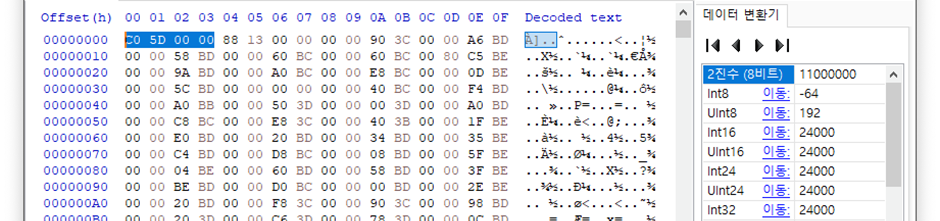

ARIA Power Trace에는 5000개의 파형이 있고 각 길이는 24000 이라는걸 알 수 있었다.
보통 전력 파형은 matplot 라이브러리 또는 matlab으로 시각화하자.
시각화를 얼마나 잘하는 가에 따라 부채널 공격 실력이 갈리기도 한다.
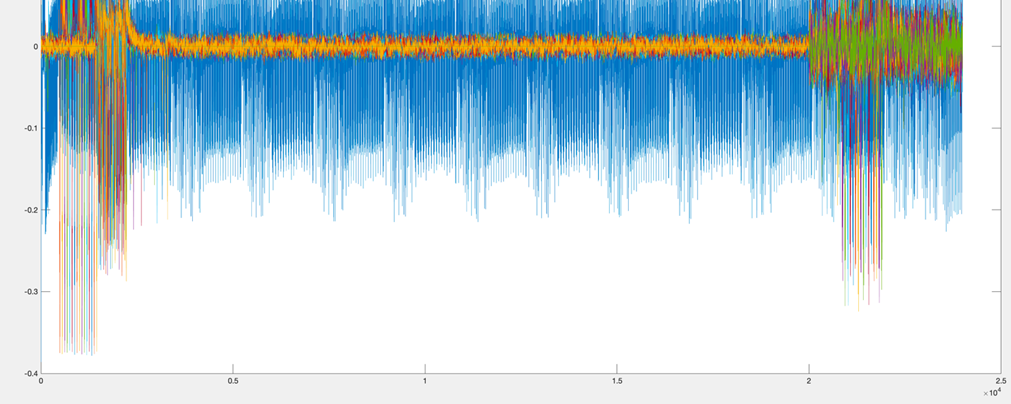
파형을 확인해보면 특정 연산이 12번 반복하고 있고 이를 통해 ARIA-128임을 짐작할 수 있다. SubstLayer, DiffLayer, AddRoundKey가 반복 중인거로 예측할 순 있지만 아직 확신할 순 없다.

ref. ARIA-128 (12 Nr), ARIA-192 (14 Nr), ARIA-256 (16 Nr)
DPA, CPA 전에는 파형을 여러개 겹쳐서 정렬이 되어있는지도 확인 해야한다.

다행히 파형은 정렬이 맞는 거 같다.
AES를 CPA할 땐 중간값의 변화가 가장 많이 큰 SBOX를 타겟으로 잡고 CPA를 했다. ARIA도 AES와 비슷한 형태를 취하고 있으며 SubstLayer에서 SBOX를 취하는 형태이다.
ARIA같은 경우 Sbox가 4개가 있는데 Sbox1 = inverse(Sbox3), Sbox2 = inverse(Sbox4) 형태를 띄고 있다. 그중 Sbox1은 AES의 Sbox와도 동일한 형태이다.
다음은 ARIA 명세서중 치환 계층(SubstLayer)에 관한 설명이다.

치환 계층 유형1은 암호화할 때, 유형2은 복호화할 때 쓰인다. 우리는 평문을 가지고 암호화 단계에서 라운드키를 찾아내는거므로 유형1만 보면 된다.
유형 1같은 경우 0, 4, 8, 12th Block은 Sbox1을 사용한다. 1, 5, 9, 13 Block은 Sbox2를 사용하고
2, 6, 10, 14th Block은 Sbox3(S^-1), 3, 7, 11, 15th Block은 Sbox4(S^-2)를 사용하는 것을 볼 수 있다.

그러면 공격할 때 블럭에 맞추어 Sbox를 달리해주면 될 거다.
우선 위 공격을 구현하기 위해 Sbox는 알고리즘 명세표에서 제공하는 4개의 Sbox로 대체한다.
편의를 위해 two dimensional array로 구성하였다.

중간 값은 다음과 같이 설정해준다.

이 상태로 CPA를 할 경우 0.9 이상으로 상당히 높은 상관계수가 나옴을 볼 수 있는데 값이 너무 클 경우 오히려 잘못된 값일 수 있으므로 상관계수 파형을 그려 확인해본다.

CB F6 D7 4C 0B 78 B9 30 22 B4 7E AA 06 E7 01 2A
다음은 찾은 키에 대한 상관계수 파형 절댓값 그래프이다. 노이즈와 상반된 값을 보이는걸 보아 옳은 키를 추측했다고 볼 수 있다.

그렇지만 여기서 끝이 아니다. 우리는 ek1을 뽑은거지, 절대로 마스터키를 추출한게 아니다.
마스터키를 알아내기 위해서 키 스케쥴링에 대해 이해할 필요가 있다.
ARIA의 키 확장 과정은 초기화, 라운드 키 생성으로 나뉜다. 초기화 과정에선 마스터키로부터 128비트의 W0, W1, W2, W3를 생성한다.
마스터키는 128, 192, 256비트 3개의 종류가 있고 어떤 크기던 상관없이 KL, KR로 쪼개지는데 128비트의 경우 KL은 상위 마스터키 16바이트(전체), KR은 하위를 채우지만 마스터키가 128비트인 관계로 0으로 채워준다. 초기화 과정은 다음과 같다.

ek1에서 W1을 알 수만 있으면 W0(KL)을 통해 마스터키를 복구할 수 있지만 지금은 W1을 알 수 없다. 따라서 다음과 같이 구해보려고 한다. 우선 ARIA는 마지막 라운드+1개 만큼 라운드키가 필요하다. 즉, 12라운드는 13개의 라운드키를 가지고 있고 마지막 라운드키는 ek13이다.

ek1, ek5, ek9, ek13, ek17은 W0 ^ (W1 >> n) 조합으로 만들어진다. 라운드키를 여러개 조합하면 W1을 알 수 있을 거 같다. 우선 우리가 구한 ek1 = W0 ^ (W1 >> 19), ek13은 W0 ^ (W1 >> 97)이다.
키 확장 파트에서 W0부터 W3까지 XOR 연산을 가지고 있기에 점멸식을 유도할 수 있다.
W0을 없애고 싶으면 ek1 ^ ek13 = (W1 >> 19) ^ (W1 >> 97), (ek1 ^ ek13) << 19 = W1 ^ (W1 >> 78)로 정리를 할 수 있다. 하지만 W0을 정리하기엔 W1을 가공해야 하므로 W1 점멸식을 사용하겠다.
W1을 없애고 싶으면 (ek1 << 50) ^ ek13 = (W0 << 50) ^ (W1 >> 97) ^ W0 ^ (W1 >> 97) = W0 ^ (W0 << 50)로
깔끔하게 정리된다.
미리 순환 쉬프트 함수를 구현해놨다.

이미 CPA를 통해 ek1를 구했으니 ek13을 구하면 마스터 키를 추출할 수 있으므로 ek13을 추출해보자

평문과 암호문을 모두 가지고 있으므로 암호문을 넣고 CPA는 동일하게 해주면 ek13의 키가 나올 것이다.
여기서 알고 가야할 점은 ek1를 추출할 땐 Sbox1 Sbox2 Sbox3 Sbox4 ... Sbox4를 1byte in 1byte out으로 반복했지만, ek13에서는 암호화 방향이 Sbox3 Sbox4 Sbox1 Sbox2 ... Sbox2 이다.
하지만 우리는 암호문(128)비트에서 key를 더해주고 Inverse Sbox를 취하는 형태로 SubstLayer까지 복호화 과정을 올라가야하므로 Sbox1 = Inverse(Sbox3), Sbox2 = Inverse(Sbox4)에 따라 그대로 Sbox1 Sbox2 Sbox3 Sbox4 ... Sbox4를 사용해주면 된다. (= 즉, ek1, ek13을 추출할 땐 입력 값만 달라질 뿐이지 CPA코드는 같다.)

9F 6B DD 65 DB 73 71 3B F8 CF 67 77 D9 D1 95 9F
ek13 키는 빨리 추출하기 위해 파형 개수를 줄이고 구간을 잘랐다. 따라서 노이즈가 ek1 cpa보다 크다. CPA PEAK의 위치를 편의상 알아보기 위해 상관계수 파형을 40% 축소해서 시각화했다.
(ek1 << 50) ^ ek13 = (W0 << 50) ^ (W1 >> 97) ^ W0 ^ (W1 >> 97) = W0 ^ (W0 << 50)
-> 12 2B A1 38 6E 1F 5E EA D5 ED 08 74 DA A9 FF 19
마스터 키(W0)과 마스터 키 >> 78 (W0 >> 78)이 XOR 되어있는 상태이다.
어차피 순환 SHIFT이기에 마지막 비트를 통해 W0의 50번째 비트를 추측할 수 있고 W0의 Shift된 값을 동시에 계산하며 전체 값을 구할 수 있다.
마스터 키의 MSB가 0인지 1인지 케이스를 나누어 복구하기로 했다.
어차피 순환 SHIFT이기에 마지막 비트를 통해 W0의 50번째 비트를 추측할 수 있고 W0의 Shift된 값을 동시에 계산하며 전체 값을 구할 수 있다.
마스터 키의 MSB가 0인지 1인지 케이스를 나누어 복구하기로 했다.
MSB가 1인 경우 10 05 44 14 01 15 10 41 04 40 00 11 14 11 14 01
MSB가 0인 경우 45 50 11 41 54 40 45 14 51 15 55 44 41 44 41 54
이 둘로는 키가 나오지 않았다. 확인해보니 홀수번째 비트만 복구되는 계산형태였다. 그러면 MSB의 바로 이전 비트까지 같이 추측해야한다. MSB로 구한 값과 MSB 이전 값으로 구한 값은 홀수와 짝수 비트를 따로 복구한 것이므로 XOR을 통해 전체 키를 알 수 있을 것이다.
마지막 비트가 00인 경우 47 72 33 61 74 4A 4F 36 59 35 55 64 49 64 69 54
마지막 비트가 01인 경우 12 27 66 34 21 1F 1A 63 0C 60 00 31 1C 31 3C 01
마지막 비트가 10인 경우 ED D8 99 CB DE E0 E5 9C F3 9F FF CE E3 CE C3 FE
마지막 비트가 11인 경우 B8 8D CC 9E 8B B5 B0 C9 A6 CA AA 9B B6 9B 96 AB

결국엔 마지막 2개의 비트가 00일 경우 나오는 키 값 (47 72 33 61 74 4A 4F 36 59 35 55 64 49 64 69 54)이 진짜 마스터 키였다.

평문과 그에 따른 ARIA 암호화 값이 같음을 알 수 있다.

MasterKey : 0x47, 0x72, 0x33, 0x61, 0x74, 0x4A, 0x4F, 0x36, 0x59, 0x35, 0x55, 0x64, 0x49, 0x64, 0x69, 0x54
ek1, ek13 조합 -> 마스터키 추출 알고리즘
key0[127] = 0; key1[126] = 0; // 값을 바꿔가며 확인
printf("case - MSB[%d] M-1[%d] -> (..%d%d)\n", key0[127], key1[126], key1[126], key0[127]);
// 홀수번째 비트추출 127 125 123 ... 1
for(idx = 127, cnt = 0 ; cnt < 65; cnt++) {
tmp[idx] = key0[idx] ^ T[idx];
if(idx < 50)
key0[idx + 78] = tmp[idx]; idx += 78;
else
key0[idx - 50] = tmp[idx]; idx -= 50;
}
// 짝수번째 비트 추출 126 124 122 ... 0
for(idx = 126, cnt = 0 ; cnt < 65 ; cnt++) {
tmp[idx] = key1[idx] ^ T[idx];
if (idx < 50) {
key1[idx + 78] = tmp[idx]; idx += 78;
}
else {
key1[idx - 50] = tmp[idx]; idx -= 50;
}
}
'Computer Security > Side Channel Attack' 카테고리의 다른 글
| [Side Channel] 부채널 공격 Overview (1) | 2024.07.24 |
|---|---|
| Linear Cryptanalysis (LC) 선형 암호 분석으로 블록암호 공격하기 (0) | 2024.05.20 |
| [Side Channel] 암호 알고리즘 부채널 분석 - AES CPA 공격 (2) | 2024.05.20 |
| [Side Channel] 암호 알고리즘 부채널 분석 - LEA CPA 공격 (0) | 2024.05.20 |
| [Side Channel] 암호 알고리즘 부채널 분석 - SEED CPA 공격 (0) | 2024.05.20 |

