Authentication and authenticated key exchanges

LaTex에 newcommand까지 넣어서 정리한게 Tistory에서는 적용 안되는 문제가 있어서 일부는 캡쳐본으로 대체합니다.

TL;DR

• 공개키 기반 인증 프로토콜 보안성 분석 논문
• 2자 상호 인증과 인증된 키 교환(Authenticated Key Exchange, AKE)에 초점.
• 따라서 개별 알고리즘 취약성보다는 프로토콜 설계상 공격 가능성을 중점적으로 다룸

Secure한 것이 무엇인가를 찾기 위해, Best Practice를 위해 관점을 넓히기 좋은 논문이기에 포스팅
학부생이 시험 공부를 위해 작성한 글이므로, 대학원생을 포함한 연구자는 생략된 점이 많기에 논문과 cross-validation 권장

1. Introduction

위협 모델

• Eve는 모든 메시지 관찰/삭제/변조/주입/재사용 및 임의 통신 개시 가능.
• 새로운 세션을 임의로 시작 가능
• 과거 통신에서 얻은 메시지 재활용 가능

2. Notation

Notation	desc
$A$, $B$	Alice, Bob (통신 당사자)	관례적 명명
${x}$	해시값 $H(x)$	중괄호는 “해시 결과” 표기
${x, y}$	$H(x | y)$	$,|, $는 연결(concatenation)
$,|, $	문자열/바이트열 연결	예: $x | y$
$s_A$	Alice의 서명용 비밀키	개인키
$s_A(x)$	메시지 $x$에 대한 Alice의 서명	서명 원문
$s_A{x}$	해시 ${x}$에 대한 Alice의 서명	해시 후 서명
$P_A$	Alice의 서명용 공개키	검증/암호화에 사용
$P_A{x}$	해시 ${x}$에 대한 공개키 암호화	공개키 암호 시스템인 경우 정의
$P_A(x)$	원문 $x$에 대한 공개키 암호화	해시 없이 암호화
$\mathrm{Cert}_A$	$(\text{Alice},, P_A,, \ldots,, S_T{\text{Alice}, P_A, \ldots})$	Alice의 이름 - 공개키 바인딩
$T$	신뢰 기관(Trusted Authority)	CA 역할
$S_T{\cdot}$	기관 $T$의 서명	예: $S_T{\text{Alice}, P_A}$
$E_K(x)$	대칭키 $K$로 $x$ 암호화	대칭 암호

Insecure simple challenge-response

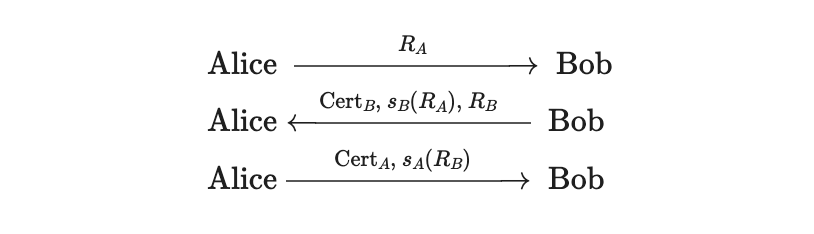
취약점: 피챌린지 측이 서명 입력에 관여하지 못함. Eve가 $R_B$를 Alice에게 중계해 $s_A(R_B)$를 받아 Bob에게 제출하면 Alice로 위장 성공.

3. Definition of a Secure Protocol

successful run의 성질

1. 두 당사자 모두 서로의 신원을 accept. 키 교환이 있으면 동일 키를 수락
2. 두 당사자가 저장한 실행 기록이 서로 매칭
3. 매칭
   • Matching Message: 한쪽 기록에서 수신된 메시지가 다른 쪽 기록에서 송신된 같은 메시지 && 인증에 관련된 모든 필드가 동일
   • Matching Records of Runs: 두 메시지를 쌍으로 묶어 매칭할 수 있고 && 각각 당사자가 자신이 보낸 순서를 서로 동일하게 유지

DoS 등으로 서비스 거부 행위 공격은 보안 침해로 간주되지 않는다.
$\rightarrow$ successful run과 secure은 구분된다.

보안성 판단 기준

• insecure run: Alice가 수락했는데, (i) 상대 기록이 매칭 불일치(일치성 위배) | (ii) 수용한 교환키를 제3자가 알 경우(키 노출)
• secure protocol: 위 조건이 항상 성립하지 않도록 (계산불능 수준) 설계된 프로토콜.

4. Desirable Protocol Characteristics

• PFS(Perfect Forward Secrecy): 비밀키가 장기 노출돼도 과거의 세션 키의 기밀성 유지
• 직접 인증(Direct): 런 종료 시점에 $K$ 지식 증명까지 완료.
• 타임스탬프 의존 X: 난수 기반 신선도 권장(시간 동기 risk)

5. Station-to-Station Protocol(STS)

STS 특성은 따로 논문을 보시길 바랍니다.

Diffie-Hellman key establish

• Alice: 비밀 $x \gets \mathbb{Z}$, 공개 $\alpha^x \bmod p$
• Bob: 비밀 $y \gets \mathbb{Z}$, 공개 $\alpha^y \bmod p$
• 공유키: $K = \alpha^{xy} \bmod p$

Basic STS Protocol

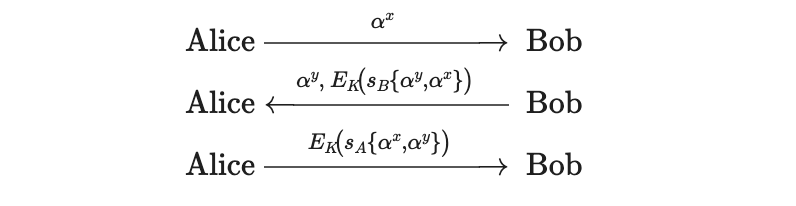
서명을 본 세션의 $(\alpha^x,\alpha^y)$와 결합, 그리고 $E_K(\cdot)$로 키 지식 증명 $\rightarrow$ 직접 인증 + PFS.

우선 Assurances부터 접근했다.

• 공유키 형성: DH 교환 후 Bob은 자신과 상대(누구일지 미확인)만 아는 키 $K$를 가짐
• 신원 문제: Alice가 이번 실행(run)의 지수쌍(그중 하나는 Bob이 이번 실행을 위해 막 생성)을 서명했으므로, 서명은 해당 실행에 결박
• 직접 인증(Direct)
  1. Alice는 $K$로 자신의 서명을 암호화해 전송
  2. Bob은 Alice가 $K$를 알고 있음(= $x$를 생성한 당사자)을 확인. Bob도 대칭적으로 동일한 보장을 얻음

여기서 이게 안전한가를 고민해보자.

Removing encryption on signatures

Modified STS: $E_K(\cdot)$ 없이 평문 서명만 교환.
서명 부분의 암호화를 제거하면, 서명된 exponential이 누구에게나 노출된다.
Eve또한 동일한 값을 서명할 수 있고 Alice의 서명을 자신의 서명으로 바꿔치기하면, Bob은 Eve를 Alice로 잘못 의식하게 된다.
즉, Authenticity breach가 발생하여 Authentication이 침해된다.

Signing only one's own exponential

Modified STS: Alice는 , Bob은 $E_K!\big(s_B{\alpha^y}\big)$

각자 자기 자신의 expoential만 서명하면 공격자가 미리 획득할 수 있는 exponential의 경우 서명 획득이 가능하다. (재사용)

RSA 서명, 해시=항등함수, DH over GF(p)

1. Eve가 $x=0$ 선택
2. $\alpha^0=1$, 공유키 $K=\alpha^{0\cdot y}=1$
3. $E_1!\big(s_A{1}\big)=E_1!\big(s_A(1)\big)=E_1(1)$ (RSA는 $1^d=1$)
4. Eve가 직접 계산 가능 $\rightarrow$ Alice 위조

즉, 공격자는 서명된 값의 이산로그 또는 서명 자체를 구할 수 있으면 키 교환에 쓰고 Alice의 서명 값을 알 수 있다. 이는 Authentication이 침해된다. 또한 replay로 인해 세션 키 신뢰성도 침해된다.

 

Signing only the other party's exponential

Modified STS: Alice는 $E_K!\big(s_A{\alpha^y}\big)$, Bob은 $E_K!\big(s_B{\alpha^x}\big)$.

상대방의 exponential만 서명하면, 공격자가 본인이 알고 있는 이산로그 값에 대응하는 공개 값을 통해 서명을 받도록 유도 가능

아까랑 같은 케이스이지만, STS를 authentication-only 프로토콜로 환원했을 때(지수 → 랜덤, 서명 암호화 제거) 다른 쪽의 값만 서명하는 경우 기존의 단순 Challenge-Response 공격에 노출됨

Uncoupling authentication from key exchange

인증을 exponential과 분리하여 서로 독립적인 값을 서명하면 MITM 공격에 취약

공격자 Eve가 Alice와 Bob 사이에서 각자 다른 지수($g^{x'}, g^{y'}$)를 삽입하면, Alice-Eve, Eve-Bob 간에 서로 다른 세션 키가 형성되고 Eve가 둘 다 알게 된다.

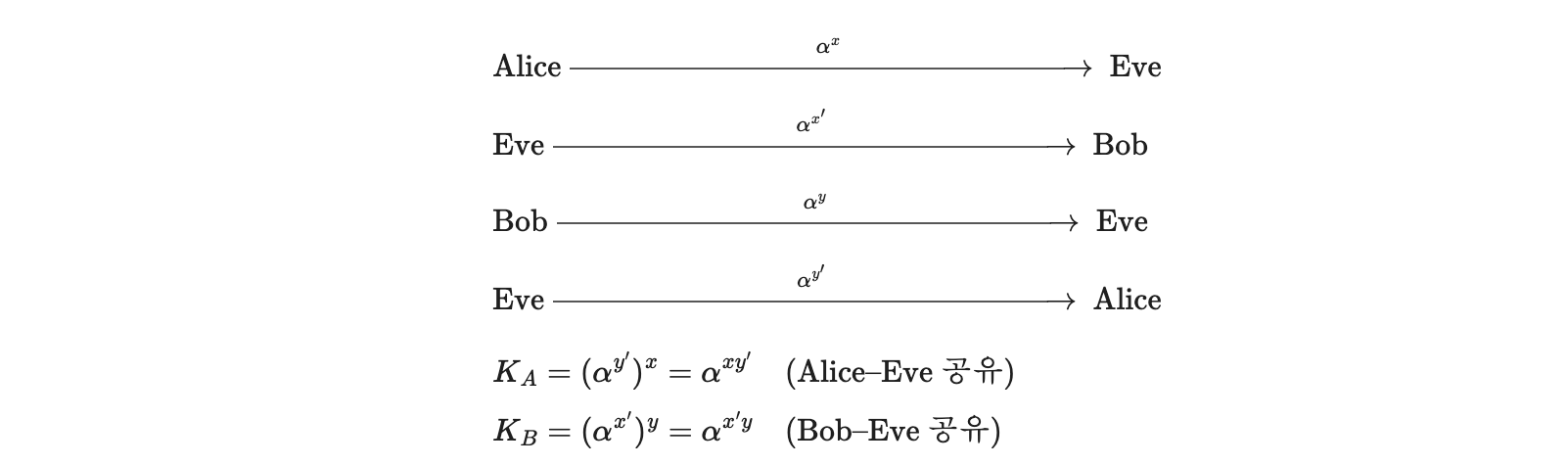
Eve는 $K_A,,K_B$ 모두 계산 가능하며 Alice와 Bob 사이의 암호화 통신을 완전히 중계, 복호화, 재암호화할 수 있다.

왜 이게 insecure이에요?

Alice는 프로토콜을 성실히 실행했고 Bob을 수락했으나, 실제로 공유된 키는 Alice가 아닌 Eve와 공유된 키였다. 따라서 insecure run이며 프로토콜 전체가 불안정하다.

이는 Authentication 자체가 무의미해지며, Confidentiality가 세션 키를 통해 메시지 내용을 노출되므로 침해된다. Eve는 메시지를 위변조할 수 있으므로 Integrity가 침해된다.

STS Protocol in Practice

1. Alice는 첫 메시지에 자신의 Diffie–Hellman 파라미터 $\alpha_A,p_A$와 $\alpha_A^{x}$를 보낸다.
2. Bob은 네트워크 고정 파라미터 대신 Alice가 보낸 $\alpha_A,p_A$를 사용하여 자신의 지수 $y$를 선택하고 응답.
3. Bob은 세 번째 메시지를 수신할 때, Alice의 증명서$Cert_A$에 포함된 $\alpha_A,p_A$와 첫 메시지에서 보낸$\alpha_A,p_A$가 일치하는지 검증.

왜 인증서에 $\alpha,p$를 포함해야 하는가?

인증서에 $\alpha,p$가 바인딩되어 있지 않으면, 공격자는 첫 메시지에서 파라미터를 substitution할 수 있음.
이로 인해 MITM 또는 precomputation index–calculus으로 연결될 수 있음.

Discussion of Other Protocols

Kerberos Protocol

대칭키 기반 프로토콜로 널리 사용되지만

• 타임스탬프 의존성: 클럭 동기화 실패 시 인증 오류 발생
• 온라인 인증 서버 필요성: 단일 장애점(SPoF) 발생
• 프로토콜 내 중복성: 불필요한 메시지 필드 존재

그외, Bellovin & Merritt 등은 추가적인 구조적 한계를 지적.

Three-pass CCITT X.509 authentication protocol

1. 불필요한 타임스탬프 필드
   • 1-2 pass 버전은 필수
   • 3-pass 버전에서는 필요없어도 필드가 남아있음
2. Alice 서명 남용 가능
   • 마지막 메시지는 $S_A{R_B, Bob}$
   • Bob의 랜덤 챌린지 $R_B$와 Bob의 이름이 결합
   • 즉, Bob이 선택한 값에 대해 Alice 서명을 얻을 수 있음
3. 옵션 암호화 필드로 키 교환 시 위험
   • perfect forward secrecy 미보장
   • 송신자가 암호화된 데이터 내용을 실제로 알고 있는지 확인할 방법이 없으므로 pass-off attack 가능
4. 서명 시스템 제약
   • 사용되는 서명 알고리즘이 서명과 암호화 둘 다 가능해야함
   • NIST, DSA와 같은 서명 스킴 사용 불가

ISO three-pass protocol

인증 전용 STS와 본질적으로 동일

1. 차이점
   • 난수의 중복 복사 허용
   • 수신자 식별 필드 선택적 포함
   • 임의 텍스트 필드 선택적 포함
2. 결과
   • 선택적 텍스트 필드를 키 설정에 사용하면 키 설정 기능 제공하지만 perfect forward secrecy(PFS) 미보장
   • 텍스트 필드 사용 시 추가 공격 벡터 가능

Attack on a specific authentication protocol

Modified: 3번째 메시지에서 Alice가 새 난수 $R_j$를 사용하고, $R_j$를 평문으로 추가 전송할 수 있음.
즉, Eve가 Alice를 가장하여 Bob을 인증시킬 수 있는 spoof, relay 공격 가능

Concluding Remarks

인증, 키교환 연계

인증과 키교환을 분리하지 말 것. 분리 시 공격자가 인증 후 키교환을 탈취 가능.
세션키 $K$를 당사자 식별자와 전체 전송문맥에 바인딩
$$K = \mathrm{KDF}(g^{ab},, ID_A \Vert ID_B \Vert H(m_1 \Vert \cdots \Vert m_n))$$

Asymmetry 유지

프로토콜 대칭성은 reflection, 재사용 공격을 유발. 양측 응답은 달라야 함.

Chaining & Freshness

각 메시지를 동일 run의 논리로 체인하고 과거/병렬 run 메시지 재사용을 차단.

nonce $N_A, N_B$, 세션ID $sid$, 타임바인딩 포함
ex: 메시지에 누적 해시 포함: $tag = H(m_1 \Vert \cdots \Vert m_i)$

Add-your-own-salt

서명, 복호 등 연산 입력이 전부 적대자 제어(adversary-controlled)가 되지 않도록, 임의값을 포함.

$Sig_A(H(\text{data} \Vert r_A))$ 처럼 당사자 선택 랜덤 $r_A$를 항상 주입

• chosen-ciphertext/queries 완화

Sparse Message Space

서명 대상은 서명함수 도메인의 희소한 부분집합이 되도록 포맷, 중복성, context를 강제.

도메인 필드 추가
ex: $\text{to_sign} = \text{CTX} \Vert \text{VER} \Vert \text{LEN} \Vert H(\text{payload})$

Notes

1. 초보자가 두 명의 서로 다른 그랜드마스터와 동시에 체스를 두면서, 한 게임에서는 백으로, 다른 게임에서는 흑으로 플레이할 경우, 각 게임에서 상대의 수를 서로 바꿔 사용함으로써 두 무승부 또는 한 번의 승리와 한 번의 패배를 보장받을 수 있다. 이로 인해 부당하게 자신의 체스 레이팅이 상승하는 결과를 초래할 수 있다.
2. 초기 버전의 X.509에서는, 마지막 메시지가 단순히 $S_A{R_B}$ 형태로 되어 있었으나, 이후의 권고안에서는 이 부분이 수정되었다.
3. RSA를 명백한 방식으로 키 교환에 사용하는 것 역시, perfect forward secrecy을 보장하지 못한다는 점

인데 개인적인 해석으로는

1. 초보자가 두 고수와 동시에 경기하면서 한쪽의 수를 다른 쪽에 그대로 옮겨두면, 실력 없이도 무승부나 비슷한 결과를 얻을 수 있다.
2. ..
3. 과거 통신이 나중에 노출될 수 있다.